Hey, wait – is employee performance really Gaussian distributed??
A data scientist’s perspective
tl;dr:
It’s probably Pareto-distributed, not Gaussian, which elucidates a few things about some of the problems that performance management processes have at large corporations, and also speaks to why it’s so hard to hire good people. Oh, and for the economists: the Marginal Productivity Theory of Wages is cleverly combined with the Gini Coefficient to arrive at the key insight.
Ahhh, it’s Q4 at Fortune 500 companies. That means it’s performance management season, when millions of employees are ranked and graded on their accomplishments over the past 12 months. Their bonuses and raises next year – or lack thereof, accompanied by a statement about their future at the company – depend on the outcome of this process.
I’ll graciously sidestep the discussion of how accurate these Fortune 500 managers could possibly be as they assess and rank their direct reports. (Accuracy here is certainly questionable, given issues such as apples-to-oranges comparisons, the principal-agent problem, the many flavors of bias, etc.). Similarly, I’ll also sidestep the negative effects that these performance management processes have on a company’s culture and work environment (don’t get me started!). Let’s instead focus on the statistical foundations of the process through the lens of a data scientist. Spoiler alert: it’s built on shaky ground.
As a quick reminder of the process at a typical Fortune 500 company, managers will annually hold a series of meetings, with the express purpose of slotting all employees into place on a “vitality curve” that looks something like this:
Dividing lines are drawn that vary from company to company, and from year to year. The categories above reflect General Electric's original 10-70-20 split from the early 1980s, which is often cited as the canonical system: the top 20% of employees are given a handsome monetary bonus, and the bottom 10% are shown the door.
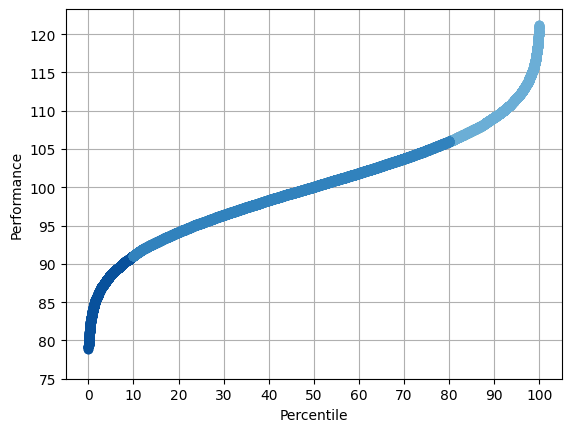
Sometimes I like to visualize the same data using a percentile chart instead – you can think of it as literally lining everyone up from shortest to tallest; each person’s “percentile” is the percent of the population that they’re taller than.
The unspoken first step here was to assume a Gaussian bell curve when it comes to employee performance. And, heck, why not? The folks in HR who were paying attention during psychology class recall that a great many things in this world follow a Gaussian distribution, including traits that have predictive power when it comes to workplace performance. IQ is Gaussian. The Big Five Personality Trait known as Conscientiousness is likewise Gaussian. For what it’s worth, human height is also Gaussian, and that’s correlated with workplace success. And it turns out that many combinations of Gaussian variables (sums, convolutions…) are also Gaussian.
Giving it the data scientist “smell test” though, a few things jump out. First, are we really paying corporate salaries to people on the low end of the bell curve? The median individual income in the US is less than $50k, so my instinct is that those in corporate jobs are likely the top half of any bell curve – not the full bell curve. Also: the symmetry of the distribution doesn’t quite line up with my lived experience. I’ve seen many employees making delightful amounts (sometimes millions of dollars worth) of positive impact, but I don’t recall that their impact was offset by the exact same number of employees on the other end of the performance spectrum, making impact of the same millions-of-dollars magnitude, but directionally… un-stellar.
A different Perspective: Pareto
As we think about the impact of an employee, measured in dollars, let’s draw a connection that I haven’t seen made anywhere else. Economists will teach you something called the Marginal Productivity Theory of Wages, the idea being that the amount of money that a company is willing to spend on an employee is essentially the value that the company expects to get out of their work. This strikes me as mostly true, most of the time, and likely to be the case in the corporate world that we’re considering here.
And then on a different day, in a different part of the microeconomics textbook, there’s often a histogram of the distribution of wages: the Pareto distribution, a mathematically interesting power-law. Let’s put these two ideas from Economics together. In any given salary band, employers across the United States are paying folks wages that collectively form a Pareto distribution:
And thus we arrive at my central idea: this is also the distribution of *performance* that we should expect from employees. Performance Management would do well to start with a Pareto assumption instead of a Gaussian assumption.
Like a good data scientist, I’m sweeping the mathematical details into the endnotes [0] so as to not befuddle the decision-makers, but fear not, the fun statistical stuff that I can’t shut up about is there in spades. Fun preview: the fact that corporate job postings these days include salary min/max lets us get an estimate of the size of a salary band, which was perhaps the piece of data that earlier thinkers who pondered such things were missing.
A Pareto distribution also passes the “sniff test” with respect to success and failure. I sometimes think that everything at a Fortune 500 company is Pareto distributed at every scale: my productivity this week, my productivity this year, the productivity of my team/project compared to others, and the success of my company compared to others. A few are quite successful, most are less successful. Supporting that notion with data is a task for another day, but let’s just say that I’ve already started the spreadsheet. In any case, let’s move forward to interpreting what we’ve discovered.
Implications
So what can be learned from realizing that performance follows this Pareto distribution?
Oh, here’s the percentile plot:
There are a few striking things here that have practical implications that inform how we might change the performance management process.
First, the Gaussian perspective holds that there is a bottom ~10% that performs egregiously poorly, and that this is an intrinsic part of the distribution. Corporations are in a constant battle to remove this portion from their payroll annually. On the other hand, looking at the Pareto percentile plot, the bottom 10% aren’t really all that different from the folks in the next 10%. As a matter of fact, there’s not an obvious place to draw a line to identify the “lowest end” employees to expunge. ~65% of employees are performing below the expectations that are associated with the salary midpoint (the green dashed line)!
But there are low-performing employees at large corporations; we’ve all seen them. My perspective is that they’re hiring errors. Yes, hiring errors should be addressed, but it’s not clear that there’s an obvious specific percentage of the workforce that is the result of hiring errors. We also know that some managers are great at hiring, and have a very low error rate – it’s a bit of a tragedy to force them to cut employees who are performing relatively reasonably.
What percentage of employees should be given extra financial rewards? Unfortunately, the Pareto plot doesn’t reveal an obvious cutpoint in this regard either. The top 35% are performing above what’s expected at the salary midpoint, so that’s a starting point. Many companies take a more granular approach than GE’s original formula, i.e. they have “good - better - best” categories for bonuses. That seems reasonable.
Regarding the very top performers, the performance management process often identifies employees who are candidates for promotion. Much like hiring errors that aren’t reflected by the Pareto distribution, I think that promotion candidates should similarly be seen as outliers. Reward them handsomely (but within bounds) since their performance is, in this case, literally off the charts, and be honest in recognizing that they’re currently being underpaid despite being at the top of the pay band. This is a small market inefficiency that the promotion will soon remedy.
Second, let’s consider what the Pareto percentile plot reveals about the process of firing and backfilling. Or more broadly, hiring in general. We can see from the performance vs frequency plot that in any given salary band, low performers are 3x as common as high performers! Wow. This aligns with my experience, and is an insight that speaks to the difficulty of hiring. And to the expected effectiveness of firing the bottom 10% and then expecting to hire people who are remarkably better.
Summarizing:
There is no intrinsic bottom 10% that needs to be expunged annually. Let managers identify any hiring errors if they think their team can do better, but don’t set a target for this number based on faulty statistical notions.
Hiring in general is difficult because low performers are 3x as common as high performers. The Gaussian-inspired idea that you’ll probably get someone better if you fire the low end is inaccurate – the most likely replacement might not be remarkably better.
Things that are missing
If someone were designing a performance management system from scratch, and they let data scientists into the room, the data scientists would likely note the following issues. These issues will all require thought, and a design that is specific to a given company (which is another way of saying that there are no easy answers that can be implemented tomorrow by everyone).
Monitoring
Any statistically driven system that results in decisions that cost lots of money should be monitored to make sure that it’s achieving its goals, and that it continues to work as time goes on. How do we know it’s working? What are our actual goals? There might need to be measures in place that let us know if the company is inaccurately categorizing people. Or if managers are hiring sacrificial lambs to protect their valued team. Or if there really is differentiation in performance between those who are being fired and those who are being kept.
Decision Theory style cost analysis
The performance management process itself requires quite a bit of time and effort. Firing 10% of the company comes with costs (severance pay). Replacing those people is also costly (a helpful order of magnitude estimate is that the hiring process all told costs the company approximately a year’s salary). That new person will statistically be with the company for, say, three to five years. Is the increase in performance greater than the cost of the entire process? Are there opportunity costs, such that the company is better off with a less intense performance management system?
A Time Series perspective
Performance management is a snapshot in time – one year. If an employee’s performance has been exemplary for three years in their current role, then has a down year, should the employee be shown the door? Would a longer term perspective on the employee’s suitability be a wiser approach?
Am I measuring what I think I’m measuring?
Data scientists worry about this a lot. (Well, the good ones do!) Is one employee's success rate lower because they’re given all of the most difficult challenges? Now you’re measuring the way that projects are assigned. Are extroverts consistently given better ratings despite equal performance? Now you’re measuring personality traits and managerial bias.
Things like this can be somewhat accounted for and watched for when designing the assessment process, but there might be trickier things afoot. It’s a manager’s job to set their employees up for success, and managers are highly unlikely to admit that they weren’t doing so, especially during performance management season when they themselves are being graded.
It’s my opinion that the biggest factor in an employee's performance – perhaps bigger than the employee’s abilities and level of effort – is whether their manager set them up for success. It’s not easy for employees to change teams to get a better manager (perhaps it should be easier!). Maybe the rate at which employees jump ship these days and get jobs at other companies is an indicator that managers aren’t giving their employees the chance to succeed.
Similarly, it’s my observation that managers who are new to a company tend to do less-than-optimally their first time through the performance management process, especially when it comes to securing preferred performance slots for the people who work under them. The inevitable gamesmanship and political horse trading inherent in the process will go down differently at each company, and the first time through the process can be a harsh learning experience. What’s being measured might be your manager’s persuasiveness in the performance management sessions, and their political capital, as much as it is a measure of your performance.
Conclusions and Outlook
Performance management, as practiced in many large corporations in 2024, is an outdated technology that is in need of an update. Abandoning the Gaussian assumption, and instead assuming a Pareto distribution reveals that there is no statistical basis for firing the bottom 10% of workers annually. Companies would be better off treating hiring mistakes as outliers, and should also think about whether it’s really worth it to fire 10% of their workforce annually. Monitoring to measure whether goals are being achieved, and cost analysis to determine if it’s worth it, are likely wise given the expenses of performance management.
I’ll also mention here that the conditions that birthed the modern performance management system (GE in the early 1980s) included an assumption of lifetime employment at a company, as long as major mistakes weren’t made. It was likely valuable, in those days, to implement some sort of carrots-and-sticks program. Forty years later, employees jump ship regularly. Perhaps withholding carrots (i.e. giving an insultingly small bonus for the lowest performers) might be enough of a stick, and healthier for all involved. Figuring all this out will take more work.
Bonus Content #1: Is there any data to support this Pareto idea?
Executive summary: yep, there’s data from the early 20th Century that’s supportive, but seems to have been forgotten. The literature basically agrees that assessing an employee’s performance is quite subjective; identifying objective numbers isn’t an easy task, but what’s out there is consistent with the Pareto view and not the Gaussian view.
Attempting to be brief so as not to lose the reader entirely:
In 1957, William Shockley (Nobel Prize winner and noted jerkwad) looked at scientific publications and patents from the early 1950s from Los Alamos, Brookhaven, and Bell Labs. His conclusion – and the data are compelling in my view – was that performance is definitely not Gaussian. His take was that the distribution is Log-Normal (a distribution that can be very similar-looking to Pareto) based on a pet theory. In 1970, Clarence Zener (yes, he of the Zener diode) in a later publication looked at Shockley’s data along with some earlier data from a couple of other publication, including “a large sample of 6891 authors, everyone, in fact, listed in Chemical Abstracts during 1907-1916 whose names started with either A or B”, and put a lot of ink into the Log-Normal vs. Pareto question, since the answer is obviously not Gaussian or anything even close to Gaussian.
More recently: Herman Anguinis has looked through data from sports, entertainment, politics, and amusingly enough, Materials Science journal publications, which makes me a part of his dataset (!). I don’t think he’s managed to put his finger on a slam-dunk dataset, but his data is directionally correct. My take on his work is that his data tends to center around total lifetime output, which speaks more to the length of one’s career than annual output, but his instincts are correct.
There are a few other references in the end notes for the curious, including a link to an AI-assisted lit search from undermind.ai.
References are all in endnote [1].
Bonus Content #2: Regarding the practice of “rolling up”
Executive summary: omg we’re unjustly penalizing ~5% of our employees and we didn’t know it. If we had a really big sample size, ~5% of employees would be placed into a higher performance tier based on their performance. We’re departing from objective standards by using a “forced distribution”.
Is there anything else that a Data Science perspective can elucidate regarding typical performance management practices? Ah yes! Let’s say that managers are sitting in a meeting evaluating a batch of 27 employees, aiming to identify the bottom 10%. That would be… 2.7 people. Someone says, “Hey, there’s no way that we can hit these percentages exactly. And what if this batch has no underperformers?”, and the response is often something like “the percentages will work out when all of the batches across the larger organization are rolled up together. So we rank-order the employees that are borderline cases, and the final cutoff lines will be drawn when everything is combined.” Everyone in the meeting nods at the idea that the Vitality Curve will emerge and all will be fair when there are enough employees batched up together. It occurs to me that this is testable with a little simulation, so I’ll believe it when I see some data! Perhaps a minimum cohort size might emerge where “rolling up” causes very little collateral damage?
Let’s simulate the performance of a cohort of Gaussian-distributed employees, and further let’s pretend that managers are miraculously perfect at evaluating employee performance, so a list of best-to-worst employees is generated in exactly correct order. (For the data scientists: AUROC = Mann-Whitney U-Test = 1). The question before us is thus: does the “rolling up” process introduce any inaccuracies? More specifically, since we secretly know every employee’s exact performance, are they correctly categorized by the process of rank ordering and drawing lines at specific percentiles?
Here is a plot of the percent mis-categorized unjustly vs. cohort size, with 32 simulated annual performance reviews for each cohort size. The Welch GE cutoffs were used (bottom 10%, top 20%). I’ve only counted the number of employees who would have been in a higher category if objective standards were used instead of rank-and-chop; the numbers basically double if we decide to also count employees who are (beneficially) bumped up a category instead of down. My takeaway here is that there’s a very good chance of mis-categorizing 2.5% of a cohort no matter the cohort size, and 5% happens commonly even if the cohort size is a couple hundred.
Endnotes
[0] Mathy Details!
Size of a pay band: when posting corporate job openings, there’s a marvelous new practice of displaying a salary band (min,max). A casual browse has revealed the tendency that a minimum salary is generally around 0.65x of the maximum, for any given pay band. This allows us to visualize the Pareto distribution within a pay band, which I haven’t seen done anywhere in the literature yet. For those looking to play along at home: a pay band of 78.1 → 121.2 is centered on 100 and has min/max = 0.65.
Pareto alpha=1.75 this was drawn from a fit to individual salary data in the US (thank you, IPUMS for the data, details below), which can also be cross-checked using the Gini Coefficient as follows: G = 1/(2a-1), where G = 0.4 is commonly cited for the US individual income (not household income!). Note that this one parameter, along with the size of the pay band, is all we need in order to specify the distribution! https://en.wikipedia.org/wiki/Pareto_distribution is a great starting place for those who wish to ponder the equations.
Gaussian sigma: the outer edges of the pay band were assumed to be 3 sigma, but using e.g. 2.5 sigma gives similar results. Toss the outliers, which is 0.27% or 1.24% of the simulated data. (Easily justified: HR has rules about staying within the pay band, and is perfectly happy to underpay or overpay folks a little at the edges). Use 7.06 for the 3 sigma scenario, or 8.48 for the 2.5 sigma scenario, fits the 100 +/- 21.2 payband.
Centering at 100 “performance units”: These plots are centered at 100 not so much to represent a salary of $100k, but rather because humans are fond of thinking of things on a scale of 0-100. A fun mathematical aspect of Pareto distributions is that they’re scale-invariant / self-similar, i.e., the dropoff from 100k to 90k is the same as the dropoff from 100 million to 90 million. So the choice of 100 is arbitrary, and the calculations work for any value that you might choose; the only quantity that matters here is the width of the pay band as a percent of, say, the minimum value. And similarly, with the Gaussian, the choice of median is arbitrary, the only thing that matters is sigma / xbar.
Plots are n=25_000
Perhaps I’ll clean up the Jupyter notebook and put it on GitHub at some point.
[1] Lit search
A few takeaways:
My reading of the more modern literature is that they’ve basically forgotten the Zener & Shockley papers, which I find to have the most compelling data. Regarding Pareto vs. Log-Normal for employee performance (and for individual income): to me, there’s not much practical difference. (I do have my own pet theory about the origin of the Pareto (or LogNormal) in these circumstances, which involves neural networks and hopefully ends with a Renormalization Group universality class, but that’s a bigger project for a later time.) Back to the literature: there are a number of other papers and articles not listed here that champion the idea of “it’s not Gaussian”, but they’re a bit short on listing concrete suggestions on what one should do once that realization sinks in.
Clarence Zener “Statistical Theories of Success” Proceedings of the National Academy of Sciences Vol. 66, No. 1, pp. 18-24, May 1970
William Shockley “On the Statistics of Individual Variations of Productivity in Research Laboratories” Proceedings Of The IRE 1957 page 279
Richard J. Chambers II “Evaluating indicators of job performance: Distributions and types of analyses” Doctoral Dissertation College Of Education Louisiana Tech University November 2016
Ernest O’Boyle Jr. And Herman Aguinis “The Best And The Rest: Revisiting The Norm Of Normality Of Individual Performance” Personnel Psychology 2012, 65, 79–119
A. Drăgulescu and V.M. Yakovenkoa “Evidence for the exponential distribution of income in the USA” Eur. Phys. J. B 20, 585–589 (2001)
A. Christian Silva and Victor M. Yakovenko “Temporal evolution of the thermal and superthermal income classes in the USA during 1983–2001” Europhys. Lett., 69 (2), pp. 304–310 (2005)
Additionally, I did an AI-assisted literature search to make sure I wasn’t missing anything big and important, which you can access here:
The data that I used to fit the Pareto to individual income (not household income!) came from the variables
INCWAGE (Wage and salary income)
ASECWT (Annual Social and Economic Supplement Weight)
from
Sarah Flood, Miriam King, Renae Rodgers, Steven Ruggles, J. Robert Warren, Daniel Backman, Annie Chen, Grace Cooper, Stephanie Richards, Megan Schouweiler, and Michael Westberry. IPUMS CPS: Version 11.0 [dataset]. Minneapolis, MN: IPUMS, 2023. https://doi.org/10.18128/D030.V11.0






You're missing a big piece of the puzzle! The main reason some companies fire the bottom X% of performers every year is to motivate everyone to work hard (if not frantically) to try to stay out of firable bucket. The system you are measuring is affected by the performance management tactics you use, by design.
In a previous life, I have both taken part in and organized annual employee rankings for a group of about 100 staff. What were the goals?
- Identify excellent performers for likely promotions, bonuses, and large raises.
- Provide information for annual raises.
- Identify those staff members who need specific guidance, training, or management to improve.
- Identify those staff members (generally only one or two) who may need to find some other place to work (possibly terminated or possibly moved for some reason to another part of the organization).
There are some features of the practical process.
- The process only works if the ranking is done by large group of near managers cross-consulting in an open (but closed to those being ranked, of course) meeting.
- There must be written evaluations of every member being ranked written in advance by the direct manager. These must be circulated well in advance to the group doing the rankings.
- The actual rankings took about 2 days of solid group meeting. No manager excused during that time.
- There are no tied ranks. We organized that by opening nominations for slot one and then, by a process of consensus, finally selecting a staff member for that slot. Then slot two, slot three, and so on.
Some observations.
- At the top, there were always several candidates for each slot and the discussions took a long time.
- Oddly, someone who might have been a candidate for slot 2, say, could fall way down after discussions and someone who was not thought to be exceptional could rise a lot during the discussions. This would sometimes happen when the phrase (or something like it) was heard:
"But didn't X work on that project beside Y?"
- The direct manager led the discussion for each candidate for each slot but it was very often comments from other managers who had seen the candidate "from the side" which were the most important.
- Wherever a staff member landed, the manager was expected to amend the original review with knowledge learned during this meeting. Sometimes the manager was specifically directed by the meeting about some point to include.
- There were often surprises. One, in particular, was of a staff member who was very good, arrogant, and hard for management to work with. However, the member happened to be, by a large margin, the most experienced on a large (maybe 15 members) group which had been given the mind-numbing task of bringing a large set of (software) libraries and tools gathered from "every which where" up to release standards. As it happened, many other managers had heard from the junior members of this group that the experienced member had been extremely kind and helpful to all of them, mentoring and teaching them constantly and never taking any credit. All the way, the direct manager had not been shown this behavior. The upshot is that the direct manager learned an important lesson that people can have more than one facet, the staff member was ranked very highly, got a big bonus and raise, and was sounded out about possible promotion. Turns out that the staff member was happy to hear about all that but really just wanted to go back to small, hard projects that could be done pretty much alone without much management. And so that happened.
- The distribution of competence clearly bulged in the middle with a long tail towards the better end. It was not a normal distribution. Only near the lower ranks did performance start to drop off noticeably. In almost all cases, the problems were either temporary (say, an accident with lots of medical treatment) or something else that could be remediated fairly easily. It was common for someone, after a year ranked at 30%, to jump up to 60, 70, or 80% just because an appropriate adjustment had been made. There were seldom such dramatic falls.
- Because of this, even the staff at the bottom of the rankings could be treated generously and fairly. During my tenure in that job, there were only one or two tagged for termination and one had already figured it out and found a job outside before the termination could even be organized. The other that I can remember may have moved on voluntarily as well. However, a few years later I worked somewhere else where that staff member had worked for a while. The member was also terminated at the new place. That suggests that mechanism had actually identified someone who was not a good worked in the field.
Finally, a word about consensus as a decision making mechanism.
The rankings were done by consensus. We did not move on from slot one until the management group (about 25 people) had agreed who was deserved that rank. Consensus does not mean a majority vote. Rather, it is a mechanism in which every voter has a veto. The discussion cannot end until every voter agrees that the decision is to stand. So long as at least one voter "vetoes", the discussion continues.
The objection is that discussions can go on for a long time. Apparently forever!
The actual effect is that a decision desired even by a large majority can be held up by a strong enough counter view. That may seem bad. But the meta-effect is even when the decision is very close (51% to 49%), if there is consensus, even the opponents agree that it is the best decision to be had. The opponents may feel it is wrong, but they will also feel that
- they and their objections have been completely and fairly heard, and
- more time and energy will not create a decision different from this one — or, at least, it would be not worth the effort to do that.
[I have also used this at other kinds of meetings to make technical decisions and it works surprisingly well. Often, if a break is taken (say, come back a week later for another discussion), the objection will vanish or the two sides will have found a new path to an even better solution. The key seems to be let every one feel that they have have been heard out and that what they have been said has been absorbed. Then the final decision can be accepted.]
The summary.
- Do prior work before the decisions (of any sort).
- A group makes the decision and consensus works. Do not rank (or promote) based on the observations of a single person.
- Rankings are not punishments. They are a way for management to figure out what needs to be rewarded and what staff needs help to do better.
- Almost every staff member has positive contributions and even those whose contributions are fairly small can get better once the roadblocks are known and addressed.
- Ranking can identify staff members who should not be part of the organization. There should not be many of those (or perhaps it is time to start ranking those who do the hiring). But the number of them should never be decided by some mechanical rule.
- Finally, fear is not a good motivation for good performance. And those who think it is should be considered for termination.
I have perhaps been lucky in my life and in my places of employment. But I was continually surprised by the good work done by those who were simply treated like human beings.
-